Recursion is the “Inception” of the computer science world. Where “Inception” metaphorically represents the concept of a dream within a dream, within a dream, etc., recursion is the concept of a method call, within itself, which could lead to an infinite loop if you’re not careful.

As with all my articles where I try and teach you concepts I’ve recently learned, there will be examples used to demonstrate these principles and to help you better understand them. My lesson on recursion is no different, and in fact, probably requires examples in order to understand the concept. But before we go into examples of recursion, there are some terminology and concepts in regards to recursion that needs to be established.

Base Case

The first of the terms is the base case. This base case is absolutely crucial to recursion because this is our escape clause. Without the base case, your code will run into an infinite loop which will cause a stack overflow. I’ll show you how to identify what your base cases will be in the examples to follow.

Inductive Step

Next up is the inductive step. The purpose of recursion is to simplify a problem, while ironically being incredibly difficult to understand itself. To understand the concept of recursion requires one to be able to identify smaller problems within the bigger problem. The catch with this concept is that in order to solve the bigger problem, the same algorithm or solution is implemented on the smaller problem over and over again. Each time the smaller problem is solved, the smaller problem is treated as a new case of the “whole problem,” and a smaller problem of the new whole problem is identified. This is continually done until the smaller problem hits the base case, where this trickle down effect of smaller problems concludes with the smallest possible problem. The smaller problems are then solved, passing its solutions upline until the final bigger problem is solved. Identifying this small problem, and by extension how to solve it is what the inductive step encompasses.

Sounds confusing? No worries, recursion itself is a confusing concept only elucidated by practice and exposure, so practice recursion in order to understand it!

This is where the diagram and code examples come in! It is especially important to plan and think the concepts over before you even write a single line of code. Let’s take a simple multiplication problem for example.

Let’s say you were asked to do multiplication, but the multiplication button on your calculator was broken, so you had to do multiplication through the addition button, it would look something like this:

Instead of 5 * 6 = 30,

You’d get 5 + 5 + 5 + 5 + 5 + 5 = 30.

The addition part of it can be done recursively! In this case, you’re multiplying 5 by n times, where for this particular example, n is equal to 6. Now how do we set this up recursively? First we need to find the smaller problem within the big problem.

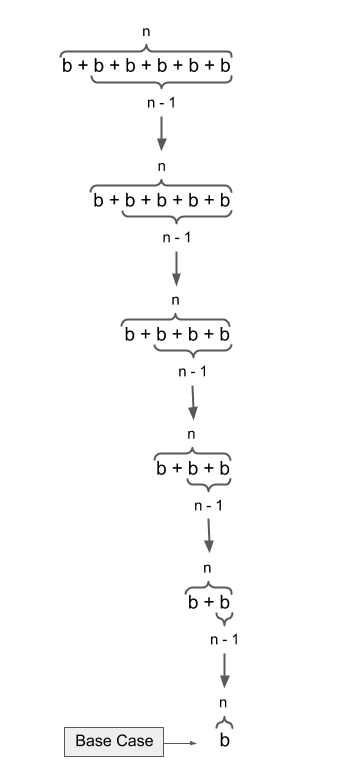
One way to look at this problem is that each smaller problem, is a new bigger problem, so as you can see from the diagram, each n-1 becomes a new n. This is the inductive step. This loop of smaller problem becoming a big problem continues until a base case is reached, in this case, where n-1 isn’t possible. Alternatively, you can also look at a problem as in the diagram below.

In the above diagram, each smaller problem is a decreasing increment from n, so instead of a series of n-1’s, you have n-4, n-3, n-2, etc. Both diagrams convey the same principles, hopefully one of them helps light the recursion lightbulb.

Now what happens when you reach the base case of a recursion problem? Usually, the base case is hard coded into the method. In the above examples, the value of b is either hard coded into the method, or passed into the method via method parameters. Let’s take a look at the code.

def recursive_multiply(b, n)
  return b if n == 1

  b + recursive_multiply(b, n - 1)
end

recursive_multiply(5, 6)

Here’s what the code looks like broken down into actual method calls.

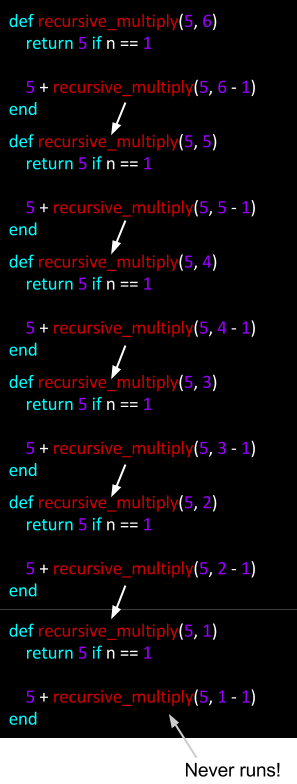
Notice that the last method call passes in an n value of 1, which is the base case. When the method is called, a 5 is immediately returned, ending the recursive loop. That returned value is then passed back up the sequence of method calls, adding the previous sum to the 5 up stream. Finally finishing the recursive method calls by passing in all the previous sums into the initial method call, resulting in a implicit return of 30. Here’s a diagram of what that looks like.

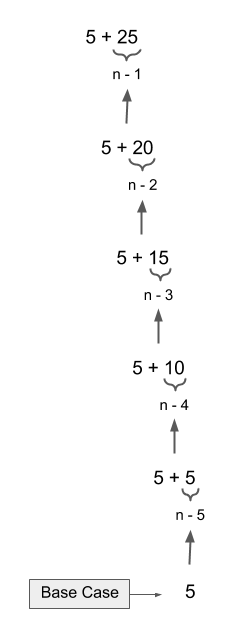
Hopefully all of this makes sense with pictures. These principles can be applied to many, many problems that involve loops such as, determining if a string is a palindrome, finding a factorial or fibonacci numbers, searching methods and even sorting methods. All you have to do is practice looking for that smaller problem. Good luck and feel free to drop any questions in the comments!